研究内容
大規模電磁場解析における反復法の高速化
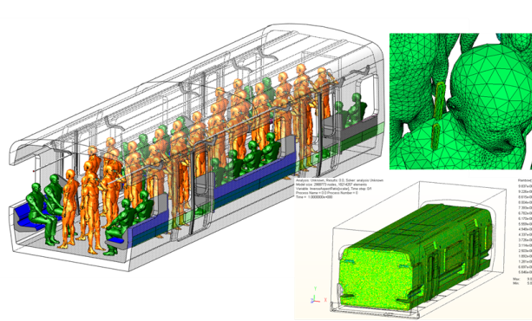
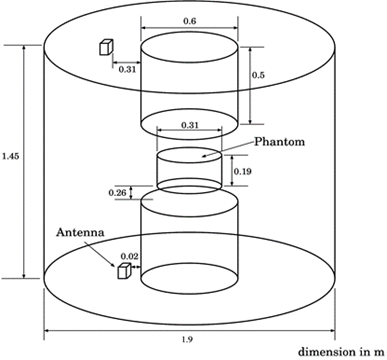
電磁場解析は身の回りの様々な電子機器のシミュレーションに用いられています. 図にあるように,携帯電話に着信があった際にその周囲の磁場を解析することによって安全性を評価したり,がん治療に使われる温熱療法の機器の設計を支援したりします. これらのシミュレーションを実現するためには大規模な連立一次方程式を解く必要があり,この方程式を解くための手法として反復法が用いられています. 性能の向上に伴い,このような解析が大規模化や複雑化すると,解析に膨大な時間がかかり,実用時間内にシミュレーションを完了できないといった問題点があります.
そこで,これらの解析の計算時間の大部分を占める反復法の高速化に取り組んでいます.
Keyword
大規模数値計算,電磁場解析,複素数問題,反復法,高精度演算,前処理
反復法における高精度演算の適用
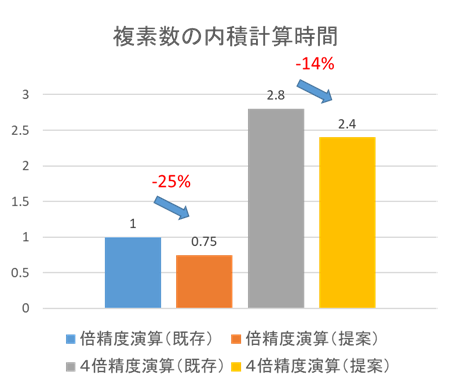
現在の計算機における数値計算は,有限桁からなる浮動小数点数によって行われており,
一般的には64bitの倍精度演算が用いられています.この数は10進数でおよそ16桁の数字を表現することができ,おおよその問題に対しては,この程度の精度で十分です.
しかし,科学技術計算分野などにおいて大規模計算が必要となる場合に,丸めによる誤差が蓄積していくことで計算結果の精度が大きく低下するといった問題があります.
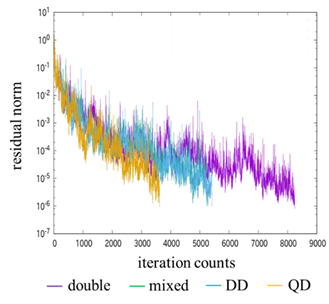
例えばここで用いられている反復法でもあるKrylov部分空間法は,その収束性が丸め誤差の影響を受けやすいことが知られており,倍精度演算では多くの反復回数,計算時間を要する場合があります.
さらに複素数問題であることから,実数の問題と比べて計算回数が多くなり,その影響もさらに増大します.
そのため,4倍精度など,倍精度よりも高精度な演算が必要となってきます.
そこで,高精度演算を複素数向けに最適化し,反復法に適用することで,反復回数と計算時間の削減を目指しています.
Performance Evaluation of Multiple-precision Conjugate Orthogonal Conjugate Gradient Method in Complex Symmetric Linear Equations
Koki Masui and Masao Ogino, Transactions of JSCES(The Japan Society for Computational Engineering and Science), Paper No.20180007,(2018)
Multiple-precision Iterative Methods for Solving Complex Symmetric Electromagnetic Systems
Koki Masui,Masao Ogino,and Lijun Liu,Lecture Note in Computational Science and Engineering, Numerical Methods for Flows(FEF 2017 Selected Contributions), pp. 321-329, (2020)
Research on the Convergence of Iterative Method Using Mixed Precision Calculation Solving Complex Symmetric Linear Equation
Koki Masui and Masao Ogino,IEEE Trans. Magn., Vol. 56, No. 1, pp. 1-4, (2020)
反復法の前処理に関する研究
反復法には,例えばCG法やCR法のような様々な解法が存在します.反復法を実装する際には前処理を施すことが一般的であり,
この前処理の種類やパラメータの値によって反復回数や計算時間が大きく異なってきます.
今回対象としている高周波電磁場問題は収束性が悪く,最適な解法が確立されていないため,特に大規模な電磁場問題向けの解法の開発に取り組んでいます.
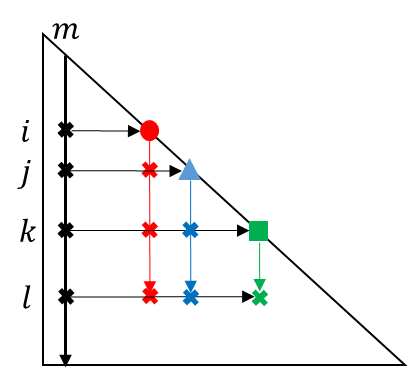
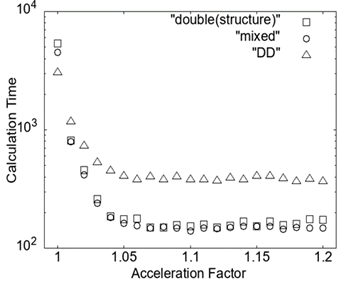
IC(𝒑) Preconditioning with Acceleration Factor for High-Frequency Electromagnetic Field Analysis
Koki Masui,Masao Ogino,Takahiro Katagiri,Fumihiko Ino,HPC Asia 2022, (2022)


